Problem 156 at Project Euler is one of the few without a specified limit. That is, most problems might ask for something like the sum of all solutions to an equation that are less than a billion. This one just asked for the sum of all solutions. When I first solved it, I just used the sum of solutions up to a trillion, which was good enough. Later I made some plots to help understand why there are no higher solutions.
Mild spoilers below if you’re thinking about trying the problem.
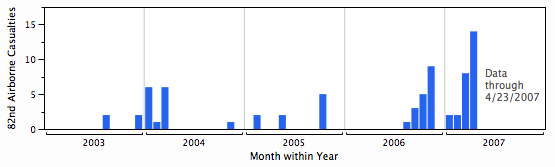
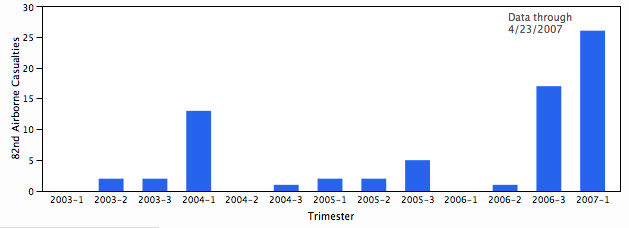
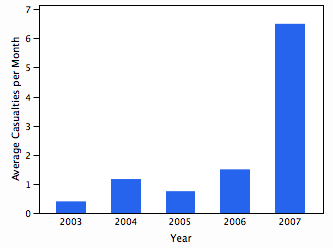
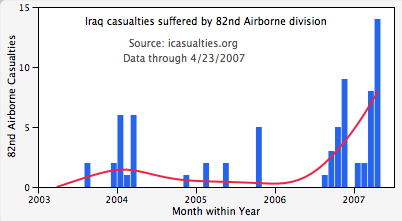
The problem is to find the solutions to f(x) = x where f(x) is the number of times a given digit, say 4, appears in all the numerals corresponding to the numbers from 1 to x. The equivalent problem is to find where f(x) – x = 0. The plots below show f(x) – x at different scales.
The first scale suggests f(x) – x for the whole range I looked at.
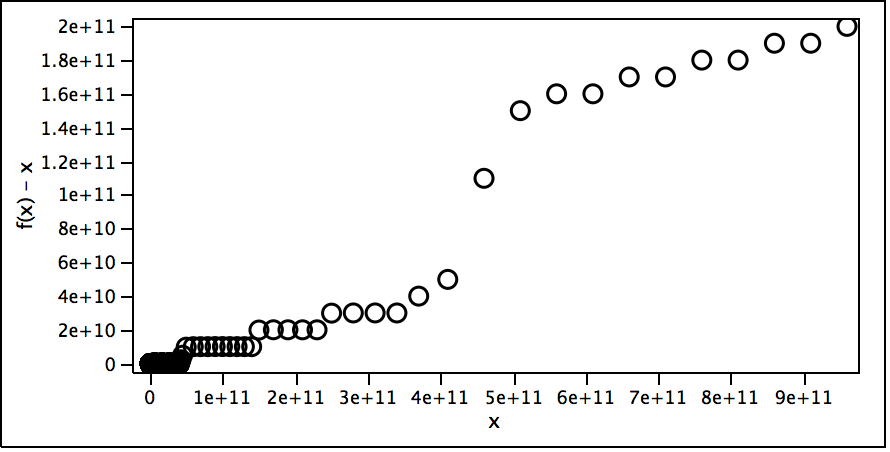
The second scale shows where the function really takes off and why. For each 1e10 range there seems to be about as many 4s as numbers (the function keeps dipping to around 0) until it gets to 4e10 when each new number in the 4e10 to 5e10 range has at least one 4 and sometimes more, so the function really takes off, especially at 4.4e10.
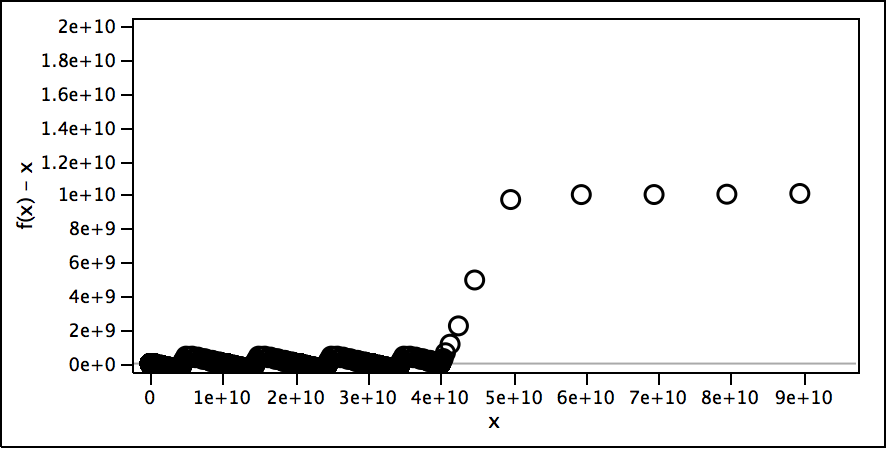
Zooming in more shows a fractal-like nature to the function.
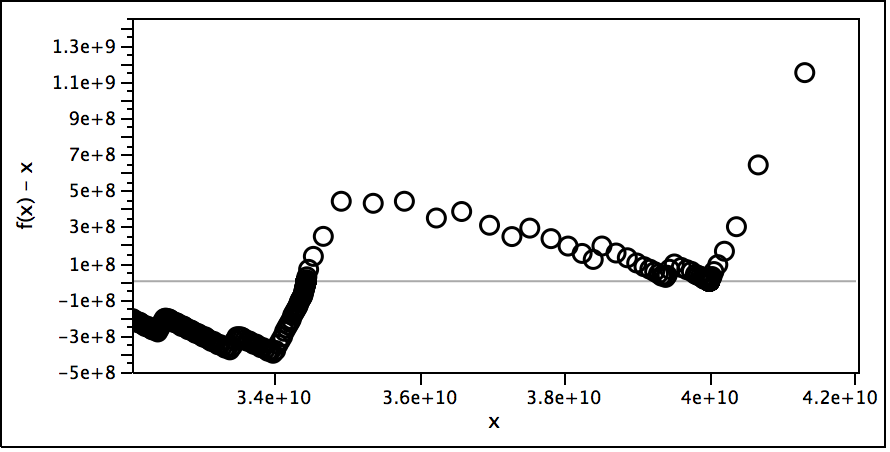
The varying density of the points is because my implementation makes fewer evaluations when further away from the origin.




 My week-end and evenings spent staring at pixels paid off as
My week-end and evenings spent staring at pixels paid off as 